Misha Kornev

Misha Kornev

PhD student in mathematics

De Bruijn Construction

4 minute read

Published:

As well known, a plane can be covered aperiodically by two types of rhombi: thick ones having angles $72^\circ$ and $108^\circ$, and thin ones having angles $36^\circ$ and $144^\circ$ (see Fig. 1).

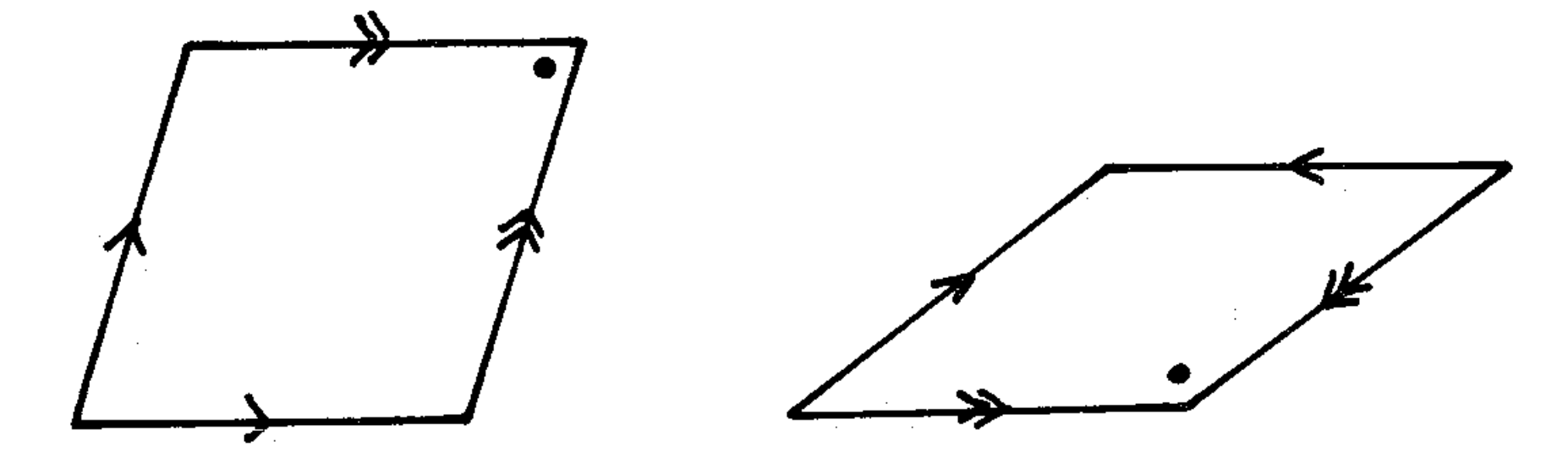
Fig. 1: The thick and the thin rhombu taken from [1]

The desired tilings appear guided by the following local rules. Two rhombi can be glued along edges with the same arrow labels and corresponding directions. Such tilings are called Penrose tilings (see Fig. 2) and have various amazing properties. First, they lack periodic translational symmetry. Second, for any two tilings, any portion of the first one can be found in the second one, just applying a parallel shift.

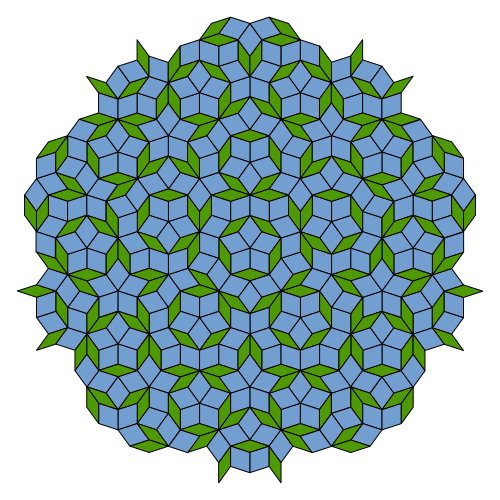
Fig. 2: A Penrose tiling taken from Wikipedia

Nicolaas Govert de Bruijn noticed that these patterns can be obtained from the following construction [1]. Start from five parallel straight lines going through the origin and corresponding to the directions along the 5th roots of unity $\zeta^j$, $j = 0, 1, 2, 3, 4$. We will refer to each of these lines as the 0th line of direction $j$. Draw other lines with step 1 parallel to the 0-th ones and enumerate them naturally by integer numbers. Now, shift each family of parallel lines by some real number $\gamma_j$ in such a way that any intersection point belongs exactly to two lines. The resulting configuration is called a pentagrid (see Fig. 3).

Fig 3: A pentagrid taken from [2]

We will call a pentagrid by de Bruijn–Penrose one if the following condition holds:

\begin{equation*} \sum\limits_{j = 0}^4 \gamma_j = 0. \end{equation*}

Notice that for each region of pentagrid (2-dimensional cell of the planar graph if you want), we can associate some 5-dimensional vector, with the $j\text{-th}$ component $K_j$ being the number of the strip which contains this region. In turn, for this vector, we consider the following point on $\mathbb{C}$

\begin{equation*} \sum\limits_{j = 0}^4 K_j\zeta^{j}. \end{equation*}

Let $S$ denote the corresponding set of resulting points when we go through the entire set of pentagrid regions. It is easy to see that in the case of de Bruijn–Penrose pentagrids, the dual graph of the pentagrid with vertices in $S$ consists of rhombi of two desired types. One can prescribe an arrow mark and a direction for each edge of this tiling in a way according to the local rules by analyzing the sums of $K_j\text{‘s}$. Thus, we see that any pentagrid produces some Penrose tiling $P.$ That’s cool!

Surprisingly, the converse is also true! Suppose we have a Penrose tiling. Consider the chain of rhombi, each of them sharing an edge of the same direction $j_0$. For each strip of rombi, let us draw a polygonal chain joining all midpoints of edges of the same direction. We get a planar graph $G$, which obviously is the dual one of $P$. It turns out that there is an isotopy of a plane making $G$ into a pentagrid.

Moreover, Penrose tilings, arising from pentagrids, are characterized by elements of the ring $\mathbb{Z}[\zeta]$ modulo some identifications. More precisely, for such a tiling with parameters $\gamma_j$, associate the complex number

\begin{equation*} \xi = \sum\limits_{j = 0}^4 \gamma_j\zeta_j^{2j}. \end{equation*}

Suppose we have two pentagrids with the numbers $\xi$ and $\xi^\ast$, producing Penrose tilings $P$ and $P^\ast$ respectively. Then the tilings $P$ and $P^\ast$ are shift-equivalent if and only if $\xi - \xi^\ast\in I$, where $I$ is the ideal generated by $1 - \zeta$.

De Bruijn also noticed that any Penrose tiling can be obtained via the orthogonal projection of some polyhedral surface in $\mathbb{R}^3$, called Weiringa’s roof (see Fig. 4). It consists of the copies of the fixed rhombus with the acute angle $\alpha = \mathrm{atan}\; 2$.

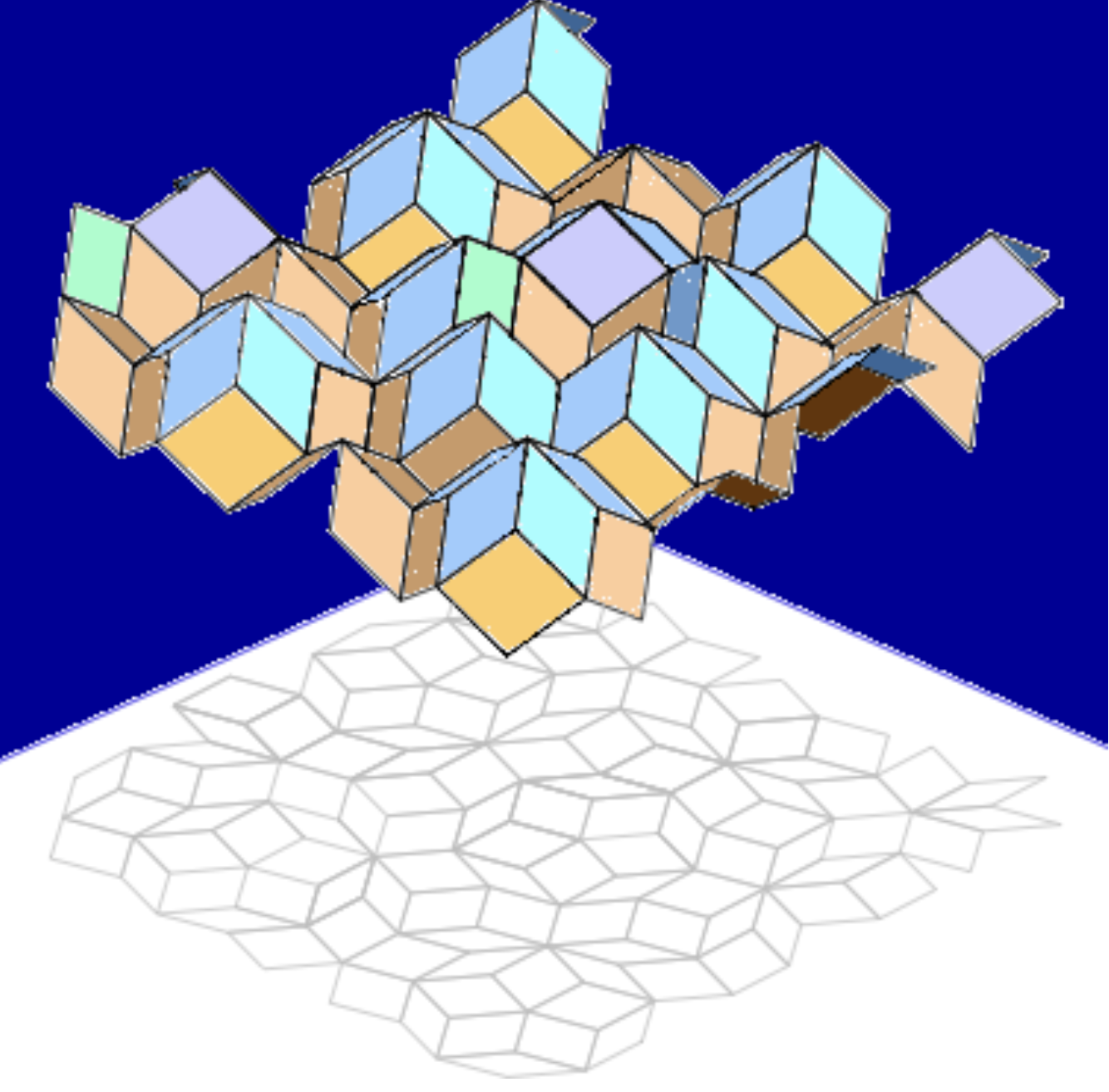
Fig. 4: Weiringa's roof taken from [2]

There are also generalizations for the cases of: non-zero sums $\sum\gamma_j$ (see Fig. 5), non-regular intersections of lines in pentagrids (see Fig.6, here, we will have tiles that can differ from rombi, e.g., decagons), mutligrids, and higher dimensions. See the excellent paper [1] for further reading.

Fig. 5: The dual of the pentagrid with $\sum\limits_{j=0}^4\gamma_j = 1/2$. Taken from [3]

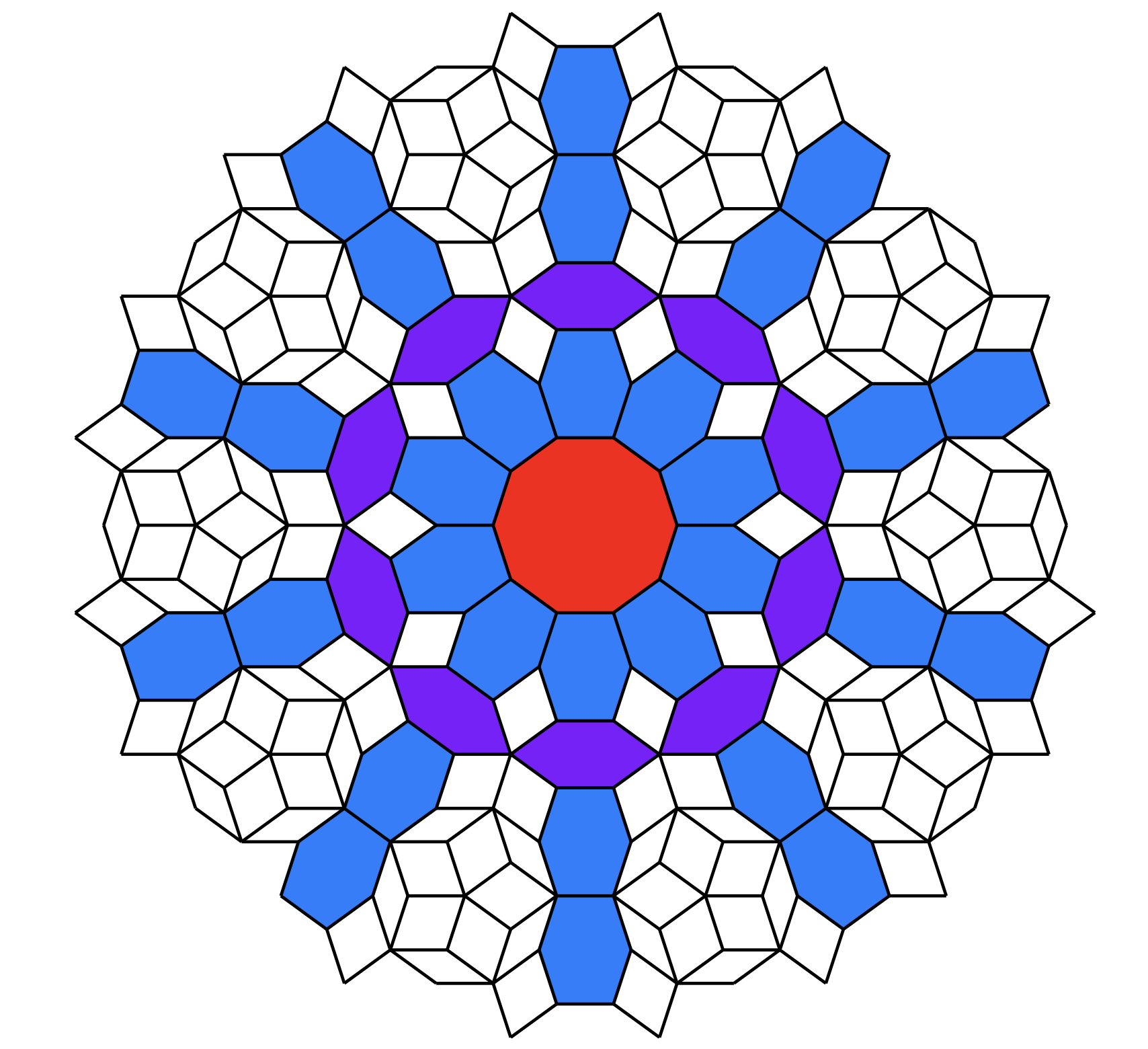
Fig. 6: The dual of the singular pentagrid with $\gamma_j = 0$ for all $j.$ Taken from [3]

References

  1. Bruijn, de, N. G. (1981). Algebraic theory of Penrose’s non-periodic tilings of the plane. I, II: dedicated to G. Pólya. Indagationes Mathematicae, 43(1), 39-66.
  2. https://www.math.utah.edu/~treiberg/PenroseSlides.pdf
  3. Bailey, Laura Effinger Dean Duane. The Empire Problem in Penrose Tilings. (2006).

You May Also Enjoy

Representation Homology

5 minute read

Published:

We can think about any commutative associative algebra $A$ as a functor $\mathcal{L}(A):\mathsf{Fin}\to k\text{-}\mathsf{mod}$ from the category of finite sets and arbitrary functions to the category of $k$-modules ($k$ is a commutative ring, the letter $\mathcal{L}$ is devoted to Jean-Louis Loday). It can be constructed as follows. On objects it is defined by sending a set $\mathbf{n}$ to $A^{\otimes_k n}$. For a morphism $f: \mathbf{n}\to\mathbf{m}$, define the morphism $\mathcal{L}(A)(f)$. Read more

Koszul Duality And Gröbner bases

3 minute read

Published:

Koszul duality is a fundamental notion of Math. Its reincarnations can be found in algebra, geometry and homotopy theory. For example, Sullivan and Quillen’s approaches to rational homotopy theory are Koszul dual to each other with respect to the Koszul duality between commutative and Lie operads. In algebra, we have the PBW-theorem (by Poincaré, Birkhoff and Witt), which states that the universal enveloping algebra of a Lie algebra looks like a polynomial algebra meaning that it has as a monomial basis of a vector space with variables being sorted by some fixed order. Further, by algebras we mean associative differential graded algebras $A = T(V)/R$ with $R$ being quadratic or quadratic-linear relations (e. g., tensor algebras $T(V),$ symmetric algebras $S(V),$ universal enveloping algebras $U(\mathfrak{g}),$ etc). Read more

Stable Homotopy Groups Via Motivic Ones

3 minute read

Published:

Briefly, there is a wonderful application of motivic homotopy theory to Agriculture classic Algebraic Topology. Classical and motivic Adams-Novikov spectral sequences coincide in the case of algebraic closed fields with zero characteristic (Marc Levine). This connection allowed to eliminate misunderstanding and mistakes in classical calculations. I will follow the Marc Levin overview. Read more

The Mandell Theorem

5 minute read

Published:

Recently, I learned about a wonderful result, Mandell’s theorem. We use algebraic invariants like (co-)homology, Massey products, Steenrod squares, etc, to prove two spaces, say, $X$ and $Y$ to be different. Anyway, each topological space can be encoded by means of some algebraic data, i. e., Postnikov’s system and $k$ invariants belonging to some cohomology groups with local coefficients — some sort of higher data. The rational part of the one, in the case of simply connected (more generally, nilpotent) spaces, can be suppressed into a commutative differential graded algebra (Dennis Sullivan’77). In general case, there are many results, contained, e. g., in the books “Rational Homotopy Theory I, II” by Y. Felix, S. Halperin, J.-C. Thomas. Read more