Koszul Duality And Gröbner bases

Koszul duality is a fundamental notion of Math. Its reincarnations can be found in algebra, geometry and homotopy theory. For example, Sullivan and Quillen’s approaches to rational homotopy theory are Koszul dual to each other with respect to the Koszul duality between commutative and Lie operads. In algebra, we have the PBW-theorem (by Poincaré, Birkhoff and Witt), which states that the universal enveloping algebra of a Lie algebra looks like a polynomial algebra meaning that it has as a monomial basis of a vector space with variables being sorted by some fixed order. Further, by algebras we mean associative differential graded algebras $A = T(V)/R$ with $R$ being quadratic or quadratic-linear relations (e. g., tensor algebras $T(V),$ symmetric algebras $S(V),$ universal enveloping algebras $U(\mathfrak{g}),$ etc).

To verify a quadratic algebra $A = T(V)/R$ being Koszul, it suffices to find a PBW-basis, i. e., a basis of $A$ with a good behaviour with respect to some lexicographical order on monomials from $T(V).$ Suppose that monomials $uvw$ of weight 3 are linearly independent, where $uv$ and $vw$ are not the leader terms of quadratic relations from $R.$ Then all ordered monomials of any length, in which each 2-letter subword is not a leader term of any quadratic relation from $R$, will be a PBW-basis of $A$. The last check can be done thanks to the “Gaussian elimination”, i. e., the Bergman-Buchberger algorithm, its upgraded version. It gives Gröbner’s basis for a finitely generated associative algebra (possibly, non-commutative). The method, based on this technique, is called the rewriting method.

Consider a clarifying example. Let $S(x, y, z)$ be a symmetric algebra on 3 generators:

Choose a lexicographic order on $T(V)$ for which $z > y > x$. In this context, the first term of each relation $r_{ij}$ is a leader term. Find all critical monomials of wight 3, i. e., such monomials $uvw$ that $uv$ and $vw$ are leader terms. In our case, such a word is unique, it is $zyx.$ Now, replace consequently $uv$ and $vw$ in all possible ways using the relations from $R$. As a result, we get some graph $G$. If $G$ is a cycle (or “diamond”) then the word $uvw$ will be called confluent. We have $zyx$ being confluent, for example (see the figure below). From the Diamond Lemma For PBW-bases and Bergman’s Diamond Lemma, it follows that $A$ is Koszul whenever any critical monomial of weight 3 is confluent. So, $S(x, y, z)$ is Koszul.

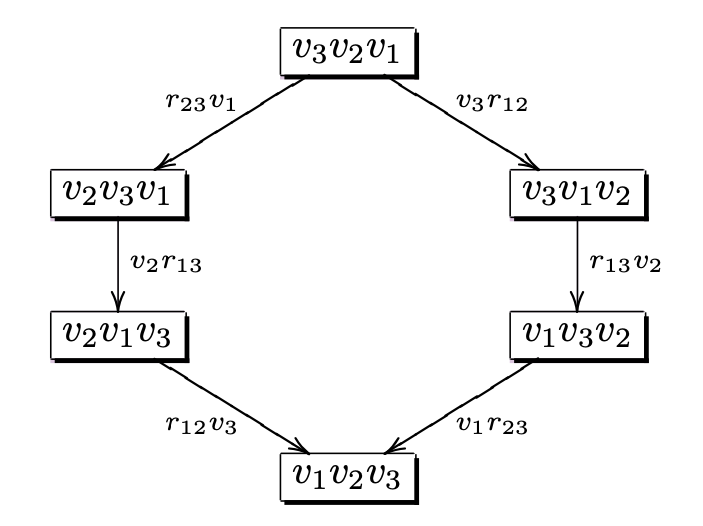
A diamond taken from [1]

Recall that Gröbner bases are useful for solving systems of algebraic equations over $\mathbb{C}.$ Via the ones, we can reduce a system to some sort of an “echelon form” and after that solve some separate polynomial equations with one variable. Basically, it is a generalization of the Gaussian elimination from linear algebra. We have a series of reductions prescribed by relations from $R$, which is an analogue of elementary row operations. Surprisingly, this idea can be pursued to the case of operads.

P. S. Also note that the Diamond Lemma is used in the proof of the uniqueness part of the normal form theorems for coproducts and HNN-extensions in group theory.

References

1. Loday, Jean-Louis; Vallette, Bruno (2012), Algebraic Operads, Grundlehren der Mathematischen Wissenschaften, vol. 346, Berlin, New York: Springer-Verlag, ISBN 978-3-642-30361-6
2. Аржанцев И. В. Базисы Грёбнера и системы алгебраических уравнений. — М.: МЦНМО, 2003. — 68 с. — ISBN 5-94057-095-X.
3. Vladimir Dotsenko, Sergey Shadrin, and Bruno Vallette, Maurer-Cartan methods in deformation theory: the twisting procedure, London Mathematical Society Lecture Note Series, 488, Cambridge University Press, 2023, 186 pp.